すごろく場「よろず屋」到達確率@オラクルベリー ドラクエ5 PS2版(DS版)
|
▲ 日記へ戻る ▲ ドラクエ5日記へ戻る ▲ メインページへ戻る |
スポンサーサイト広告(提供:Amazon) |
はじめに
このページは、オラクルベリーのカジノ地下にある「すごろく場」で、「よろず屋」のマスに止まれる確率を計算したものです。
この「よろず屋」では、(ばくだんいし)(ファイトいっぱつ)という、通常このタイミングでは手に入らないアイテムが購入可能であり、この確率は、やり込みの戦略に影響を与えます。なお、計算過程の説明も後半に付記しています。ドラクエに関係ない、単なるすごろくの計算手法としても参考になるかもしれません。
追記:2011.10.24 「ふりだしに戻る」を利用するリカバリーに関する記述を追加しました。
追記:2011.10.28 「ふりだしに戻る」を利用する方針での厳密計算、「?」を利用する方針での記述を追加しました。
まとめ
目的
(すごろくけん)の所持数に応じた、「よろず屋」に到達できる確率を算出する。
ただし、この所持数には、「すごろく場」のタンスのものは含まない。すごろく挑戦前に所持している数である。
仮定
・サイコロの出る目は、1~6が等確率として計算。
・途中の敵出現で全滅する確率は0として計算。
・途中でGがなくなって失敗となる確率は0として計算。
・「?」に止まった時に「ふりだしに戻る」の効果が出る確率は、1/8として計算。
※この1/8は、適当な値であるが、「?」は狙わない方針が前提のため、結論に示した確率には影響を与えない。
詳しくは後述されています。
結論
「ふりだしに戻る」と「?」を狙わず、スタートから直接「よろず屋」を狙う方針で挑戦を繰り返す場合は次のようになる。
| すごろくけん所持数 (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| よろず屋到達率 (Ptotal) | 0.289 | 0.487 | 0.626 | 0.725 | 0.797 | 0.849 | 0.887 | 0.915 | 0.936 | 0.952 |
| すごろく場内の券回収なし前提 | 0.242 | 0.426 | 0.565 | 0.670 | 0.750 | 0.811 | 0.856 | 0.891 | 0.918 | 0.938 |
すごろく挑戦1回ごとの確率 (2011.10.24、28 追記)
■挑戦1回ごとの「よろず屋」への到達率は、方針により異なり、次のようになる。
α = 0.242158922 スタートから直接のみ狙う
σ = 0.252706137 「ふりだしに戻る」も狙う (0.010547215 の確率向上)
Σ = 0.2585 「ふりだしに戻る」「?」ともに狙う (0.0058 の確率向上) [推定確率1/8を使用して計算]
■サイコロを振った回数ごとの「よろず屋」到達率は次のようになる。
|
表2:サイコロ回数と到達率(スタートから直接のみ狙う)
|
表3:サイコロ回数と到達率(「ふりだしに戻る」も狙う)
|
■以下は、挑戦1回ごとの各事象の確率である。(α、σ、Σについても再掲)
α = 0.242158922 スタートから直接、「よろず屋」に到達する確率
β = 0.231374314 スタートから直接、(すごろくけん)のタンスに到達する確率
γ = 0.041863736 スタートから直接、「ふりだしに戻る」に到達する確率
δ = 0.21563(+0.0001程度の誤差) スタートから直接、「?」に到達する確率[近似計算]
ε = 0.02710 = δ×(1/8) スタートから直接、「?」に到達し、スタートに戻る確率[推定確率1/8を使用]
σ = 0.252706137 「ふりだしに戻る」も狙う方針で、「よろず屋」に到達する確率
Σ = 0.2585 「ふりだしに戻る」「?」をともに狙う方針で、「よろず屋」に到達する確率[推定確率1/8を使用]
※スタートから直接、とは、「ふりだしに戻る」「?」を一度も経由しないことを意味する。
※「ふりだしに戻る」を狙うのは、直進すると「よろず屋」を通り過ぎるサイコロの目が出た場合のみとする。
※「?」を狙うのは、「よろず屋」または「ふりだしに戻る」を通り過ぎた場合のみとする。
補足
■「すごろく場内の券回収なし前提」の確率
結局、「すごろくへの挑戦回数」と「よろず屋への到達率」の関係を表しています。
また、次のような場合にも使える数値です。
(すごろくけん)を5枚所持して挑戦
→すごろく場内のタンスにある(すごろくけん)を回収できて合計6回挑戦したがクリアできなかった
→本来回収する予定のなかった、宿屋2Fと防具屋2Fのものを2枚回収して再挑戦する
→この場合「すごろく場内の券回収なし前提」にあてはまるので、この状態からの突破率は0.426
挑戦1回ごとに時々刻々と変わる「この時点からの突破率」を把握する際にも使えます。
■「ふりだしに戻る」「?」を期待したリカバリー について (2011.10.24、28追記)
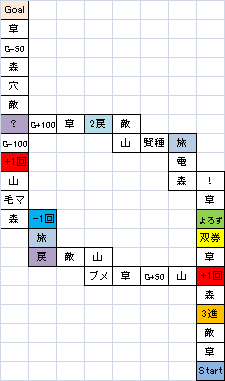
「ふりだしに戻る」は、スタートから12マス目にあります。5マス目の「分岐点」を左折した場合のみ狙えます。
また、「よろず屋」は、スタートから8マス目にあります。5マス目の「分岐点」を直進した場合のみ狙えます。
5マス目の分岐点の前で振ったサイコロの目が大きく、「よろず屋」を通り過ぎることが確定した場合には、左折して「ふりだしに戻る」に止まることを期待すれば、「よろず屋」に到達できる可能性が残ります。
また、「?」は、スタートから20マス目の合流点にあり、ここでは低確率で「ふりだしに戻る」効果が発動することがあり、「よろず屋」「ふりだしに戻る」を通り過ぎた場合に同様の効果が期待できます。
しかし、両リカバリー策ともに、戦闘の発生率が上がるため、タイム的な期待値は「やめる」を選んでやり直した場合よりも悪くなると筆者は考えております。このため、本ページの結論の項では「ふりだしに戻る」「?」を期待したリカバリーは狙わない前提での確率を計算しています。
ただし、最後の1枚の(すごろくけん)を使った挑戦のような場合は、間違いなく有効に機能するリカバリー策になります。
なお、12マス目の「ふりだしに戻る」を狙うリカバリー策については、腹黒パンダさんのblog記事に記述があり、筆者はそれを読んでこの分岐に気づきました。
■すごろくけん 所持数について
このすごろくに初めて挑めるストーリー進行度で回収できる(すごろくけん)は通常7個です。このうち、比較的タイムロスが少ないもののみ回収すると5個となります。(最初の船2、古代の遺跡1、ヘンリー1、カジノ地下1)
また、コロマージが宝として落とすことがあるようです。
(参考:ドラゴンクエストV 天空の花嫁公式ガイドブック上下巻プレイステーション2 版)
■サイコロを振れる回数
10回です。ただし、止まるマスにより、これが変動する可能性があります。
計算の流れ
すごろくけん の所持数だけ複数回挑戦した後の確率計算 1,2,3,4
| マスの属性 | ID | |
| 進 行 方 向 ↓ | スタート | 0 |
| 1 | ||
| 2 | ||
| 3マス進む | 3 | |
| 4 | ||
| 分岐点 | 5 | |
| 6 | ||
| すごろくけん | 7 | |
| よろず屋 | 8 |
1.よろず屋に到達しない確率
2.よろず屋に到達しない、かつ、すごろくけんを取れる確率
3.すごろく場で取得した(すごろくけん)を使った最後の挑戦で、よろず屋に止まる確率
これは2の確率に、1回分の到達率をかけて得られる。
1と3の確率から、全到達率を算出できる
上述2の計算のために必要な量
4.よろず屋に到達しない、かつ、すごろくけんを取れない、確率
1から4を引いて、2を得る
挑戦1回ごとの確率計算 a,b,c
1.のために必要な量
a よろず屋に到達しない確率
4.のために必要な量
b よろず屋に到達しない、かつ、すごろくけんを取れない、確率
b のために必要な量
c よろず屋に到達しない、かつ、すごろくけんを取れる 確率
aからc引いてbを得る
※上記cは、マス目の順番から、すごろくけん取れたのち、よろず屋に止まれない、と解釈でき、計算が楽
このため、bよりもcが求めやすそうと判断した。
計算式
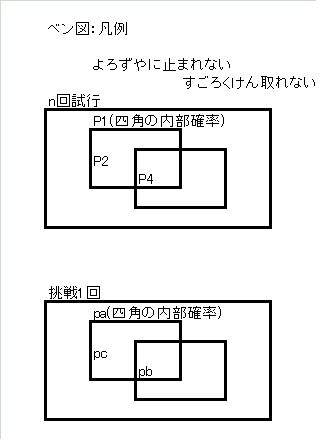
すごろくけん 所持数は n とする。
P 複数回施行後の確率
p 挑戦1回ごとの確率
それぞれ添え字を打つ。添え字は、上述に対応。
全到達率はPtotal
Ptotal = (1-P1)+P3
P1 = pa^n
P2 = P1-P4
P3 = P2×(1-pa)
P4 = pb^n
pa = 0.757841078 別途計算した値。過程は後述
pb = pa-pc
pc = 0.192811928 別途計算した値。過程は後述
以上より、計算に必要な基礎パラメータは、2つである。
pa,pc である。
その後の計算は、pbからP4を求めるところが考え方の中心。
なお、上記を代入すると、結局paとpcのみの以下の式を得る。
Ptotal = (1 - pa^n)+{ pa^n - (pa-pc)^n }×(1 - pa)
基礎パラメータ pa pc の計算
計算結果
pa = 0.757841078 = 1-α
pc = 0.192811928 = β×(5/6)
参考パラメータ:
α = 0.242158922 よろず屋に止まれる確率
β = 0.231374314 すごろくけんに止まれる確率
計算方針
・行列 A オラクルベリーすごろく行列
・ベクトル vk k回サイコロを振ったあとの、所在マス目の確率分布ベクトル
として、Aによる、vkの時間発展を調べる方法で計算しました。
計算方法の説明
たとえば、スタートから1回だけサイコロを振ったあと、どういう状態になっているでしょうか?
サイコロは1~6の目が出るので、1/6の確率で、1~6マス目にいる・・・かと思いきや、オラクルベリーのすごろく場には、3マス目に「3マス進む」のマスが配置されているため、実際は次のようになります。
| マスの属性 | ID | 確率 列ベクトル v1 |
| スタート | 0 | 0 |
| 1 | 1/6 | |
| 2 | 1/6 | |
| 3マス進む | 3 | 0 |
| 4 | 1/6 | |
| 分岐点 | 5 | 1/6 |
| 6 | 2/6 | |
| すごろくけん | 7 | 0 |
| よろず屋 | 8 | 0 |
つまり、「1回サイコロを振った後の状態」は、右列の確率分布、すなわち「列ベクトル」ひとつで表されることになります。
同様に、「k回サイコロを振った後の状態」の確率分布も、ひとつの列ベクトル vk で表すことができます。
さて、次にこの「1回サイコロをふる」という操作を、行列との積をとる操作として考えてみます。
ためしに、v1=A v0 を満たす、行列Aを考えてみます。
| v1 | = | A | v0 | |||||||||
| 0 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | 1 | ||
| 1/6 | 1/6 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 1/6 | 1/6 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 0 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 1/6 | 1/6 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 1/6 | 1/6 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 2/6 | 2/6 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 0 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
| 0 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ||
つまり、0番目のマスから移動する場合の、移動先の確率は、行列Aの0列目に書いておけばよいことになります。
同様にして、j 番目のマスから、i 番目のマスに移動する確率を、 i 行 j 列成分に書いていけば、これがオラクルベリーのすごろく場において、確率分布の時間発展を決める行列Aになります。
(便宜上、行、列の開始を0からとしていることに注意)
分母の1/6はすべてに共通するので、外に出しておくと、Aは次のように定義されます。
| 0 | 0 | 0 | ※ | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | ※ | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | ※ | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | ※ | 0 | 0 | 0 | 0 | 0 | |
| A = 1/6 × | 1 | 1 | 1 | ※ | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | ※ | 1 | 0 | 0 | 0 | 0 | |
| 2 | 2 | 2 | ※ | 1 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 1 | ※ | 1 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 1 | ※ | 1 | 1 | 1 | 1 | 0 |
この行列を用いれば、 v2 = A v1 以下、
vk = A vk-1 により順次、確率分布ベクトルが定まります。結局、以下の式を得ます。
vk = A^k v0
なお、3マス目には止まることがないので、対応する列の成分は定義できません。実際、何が入っていてもよいです。
また、この3マス目に対応する行も列もそもそも必要ないので、消して8×8行列にしてしまっても支障はないです。
最後に確率計算です。
よろず屋のマスに止まる可能性があるのは、サイコロを2~7回振ったときなので、
それぞれの回数サイコロを振ったあとの、確率分布ベクトルの和を取ればよいです。
vtotal = v2+v3+・・・+v7 の、一番下の成分が、よろず屋に「止まれる」確率αになります。
これを1から引いて、paを得ます。
実際の計算では、
vtotal = v2+v3+・・・+v7 = (A^2+A^3+・・・+A^7)v0
なので、A^2+A^3+・・・+A^7 の左下スミの成分の和を取って計算しました。
すごろくけんの回収率についても、ほぼ同様の計算で算出できます。
「止まれる」確率βに、次のサイコロの目が1以外となる(=よろず屋に止まれない)確率5/6をかけ、pcを得ます。
なお、数値計算はすべてエクセルを用いて行っています。
付録 「ふりだしに戻る」、「?」を狙う方針での確率計算
付録1 γ=「ふりだしに戻る」に到達する確率 (2011.10.24追記)
γ = 0.041863736 スタートから直接、「ふりだしに戻る」に到達する確率
計算した結果は以上になりました。
これを踏まえ、「ふりだしに戻る」を期待したリカバリーを狙う方針の場合、γ×α = 0.0101 より、
概算で『挑戦1回ごとの「よろず屋」到達率』は、 1.0% 程度、向上すると考えられます。
以下は γ の計算過程です。
合理的に判断すると、「ふりだしに戻る」に狙いを変更するのは、次の場合に限られます。
(i) 4番目のマスに止まっているときに、サイコロの目が5か6である。
(ii) 5番目のマスに止まっているときに、サイコロの目が4か5か6である。
これを踏まえ、『合理的な場合には、「ふりだしに戻る」も狙うすごろく行列』 B を定義すると、次のようになります。
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B = 1/6 × | 2 | 2 | 2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
確率分布ベクトルは、0~12マス目に対応する13成分となるので、13×13行列になります。
9~12マス目にあたる青地の部分が、行列Aにつけ足された形です。9~12マス目は、左折したあとのマスが対応しています。
あとは同様の計算をして、γの値を得ています。もちろん、この行列からα、βも得られます。
なお、このγを用いて、リカバリーを狙う方針での突破率を厳密に計算するのは簡単ではありません。
問題1 サイコロの回数が尽きている可能性 サイコロの回数は変動する
問題2 2回以上「ふりだしに戻る」を経て、つまり複数回ループして、「よろず屋」に到達する可能性もある
という事情があり、状況が一気に複雑化するためです。
しかし、これら2つの問題を解消し、厳密な計算することも可能です。付録2、付録3で、その方法を用いて計算を行います。なお、以下で行う厳密な計算では、結局 γ の値は使用しません。
ただし、上述した 「+1.0%の向上」は、かなり良い近似になっているので、実用上これで支障はありません。
付録2 複数回ループの計算方法 問題2の解消 (2011.10.28追記)
付録1示した議論から、問題2を解消してさらに厳密に計算することが可能です。
行列Bで、「ふりだしに戻る」への到達率を求めるために設定していた「12マス目」に対応する12行目の成分を、0行目に移すことで、そのままスタート地点に戻る確率を表現できます。
この行列 B ' を累乗計算し、よろず屋に到達する成分の和を取ればよいだけです。
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B ' = 1/6 × | 2 | 2 | 2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
この計算方針でも、問題1は解消されておらず、サイコロの回数が尽きる可能性があります。
振ることのできる回数は一定せず、10回~15回のいずれかになるので、何乗の成分まで和を取ればよいのかわかりません。
したがって、これだけでは挑戦1回あたりの「よろず屋」到達率は厳密には計算できません。この問題1の解消方法については、付録3に示し、そこで厳密な値を計算します。
ちなみにこの計算の結果も、十分実用的には耐えうる精度となります。
0.252626989 サイコロを10回振れるとした場合
0.252737877 サイコロを15回振れるとした場合
付録1での近似計算「+1.0%の向上」が良い近似であったことがわかります。実用上は、スタートに戻るループは、1回まで考慮すれば十分ということが確かめられた結果となりました。
付録3 サイコロ回数変動の計算方法 問題1の解消(2011.10.28追記)
前述のように、サイコロを振れる総回数を変動させるマスの存在により、行列の何乗までの和をとればよいのかがわからなくなります。
これは行列を拡張することで対処することが可能です。これによりやっと、「ふりだしに戻るを狙う方針でのよろず屋到達率」 σ の値が厳密に計算できます。なお、厳密という言葉の意味は、このページで用いている意味においてです。サイコロの目の等確率など仮定が崩れている場合はこの限りではありません。
結果は次のようになります。
σ = 0.252706137 「ふりだしに戻る」も狙う方針での、「よろず屋」到達率
計算方法は単純です。「振れるサイコロの総回数」の分岐の数だけ、すごろく場そのものが存在すると考えます。
そして、「サイコロの回数+1回」とかなったら、「サイコロを11回振れる別のすごろく場」の同じマスにワープしたと考えればよいです。サイコロの振れる回数は、10回~15回になるので、6つのすごろく場を想定すれば済みます。
必要ないマスに相当するベクトルの成分を消すと、必要な成分は11個です。これを6つのすごろく場の分考えて、11×6=66
つまり、66次元ベクトルを使えば、「現在いるマス目」「サイコロを振れる回数」の両方を含めた確率分布が表せます。
このベクトルの時間発展を表すには、66×66行列があればよいです。任意の2状態間の遷移確率を定義して行列を作り、それを15乗すればよいです。
この場合、「よろず屋」に止まる確率は、6つのすごろく場においてありえるので、6つの成分が対応します。
ただし、それぞれサイコロを振れる回数が異なるので、行列の10乗~15乗の適切なところまでの和を取る必要があります。
こうして得た6つのすごろく場での確率の総和を取れば、全体の到達率が厳密に計算できることになります。
なお、計算チェックとしては、以下の3つを確認しました。
・近似計算との比較
・すべてのすごろく場で15回までの和をとると、付録2の15回の値と同じになる
・計算過程で、「15回のすごろく場に、サイコロを13回振った時点で入ってくる」のは5マス目のみで、81通りであった
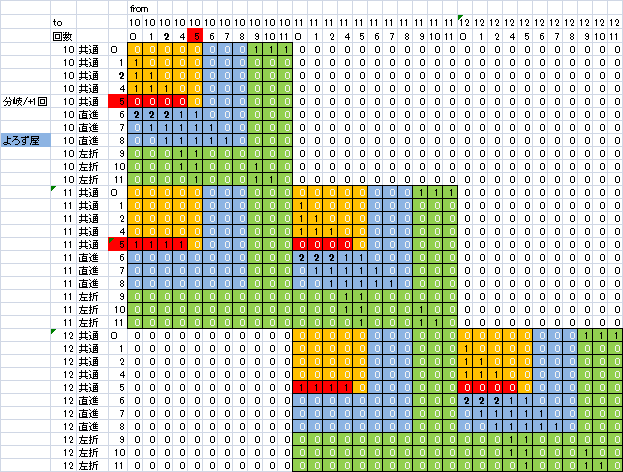
実際に計算に用いた行列を下に示します。画面の都合上、全体の1/4にあたる33×33のみ示しますが、この外側に繰り返しで広がっていきます。
確率になおすには、値にすべて1/6をかけます。
赤地のところが、サイコロ回数の遷移にあたる「別のすごろく場へのワープ」的な成分になっています。
付録4 δ=「?」に到達する確率 (2011.10.28追記)
結果は次のようになります。
δ = 0.21563(+0.0001程度の誤差) スタートから直接、「?」に到達する確率
計算過程は、例のごとく行列の累乗です。この計算に用いた行列は、この節の最後に示しますので、興味がある方はご覧ください。
スタートから20マス目にある「?」のマスに止まり、「ふりだしに戻る」効果が出れば、それでもリカバリーが可能なので、これを狙う方針でプレイすれば、「よろず屋」に止まれる確率はわずかに上がります。ここで求めた δ の値は、この計算に使えます。
この「?」のマスによるループも、実際は複数回起きた上で「よろず屋」に止まれることがあり得るのですが、それを考慮しても実用的な意味がほとんど生じないことは、付録1~3よりわかりますので、ここでは「付録1」で行った水準までの近似計算に留めたいと思います。厳密な計算については、付録5でアイデアのみ紹介します。
上記の計算結果は、サイコロ9回以内で「?」に到達する確率です、サイコロを10振れる、11回振れる可能性もあり、この場合はその分が加算されます。なお、12回振って「?」に止まる可能性がありますが、これは「よろず屋」に到達するには回数が足りないため意味がありません。
参考までに、各サイコロ回数に対応する「?」到達率を以下に示します。
| サイコロ回数(n) | 確率 n 回目でちょうど 「?」に到達 | 確率 n 回目までに 「?」に到達 |
| 3以下 | 0 | 0 |
| 4 | 0.032407407 | 0.032407407 |
| 5 | 0.071630658 | 0.104038066 |
| 6 | 0.062778635 | 0.166816701 |
| 7 | 0.032853938 | 0.199670639 |
| 8 | 0.012284355 | 0.211954994 |
| 9 | 0.003678420 | 0.215633415 |
| 10 | 0.000967185 | 0.216600600 |
| 11 | 0.000241945 | 0.216842545 |
さて、ここで「21.5%って、ずいぶんの高確率じゃないか!」・・・と喜んではいけません。
これは単に「?」に止まる確率であって、スタートに戻るには、さらに「?」の複数の効果のうち、ふりだしに戻る効果が出なくてはなりません。
この確率は調査していませんが、ドラゴンクエストVのあるきかた によると、ここで出る効果は全部で8種類のようです。
そこで、これらの効果が等確率で起きると仮定し「ふりだしに戻る」効果が出る確率は 1/8 という仮定のもとに計算してみます。
ε = 0.02710 = δ×(1/8) 推定確率1/8を使用
これが、「?」のマスを使ってスタートに戻れる確率になります。2.7%程度と、結構高い確率です。
しかし、ここでもまだ喜んではいけません。スタートに戻った後に、サイコロを振れる回数が十分に残されているかわからないからです。残り回数と、「よろず屋」到達率については、「まとめ」にある表で述べたとおりです。
サイコロを振れる回数が不確定なので、適当に設定し、
「?」に8回以内でまず到達、以降「よろず屋」に3回くらいで到達 という前提で計算すれば
0.005887 = 0.211954994 × (1/8) × 0.222222222
0.58%程度、「よろず屋」に到達できる確率が向上することがわかりました。
この程度の議論で近似計算を終えたいと思いますが、実用の精度としては問題ないでしょう。これ以上、計算上で厳密さを求めるよりも、上で使った「推定確率1/8」を精度の良いものに取り換えるための調査の方がはるかに重要そうです。
ただ、さらに厳密な計算手法が気になる方には、付録5の記述が参考になるかもしれません。
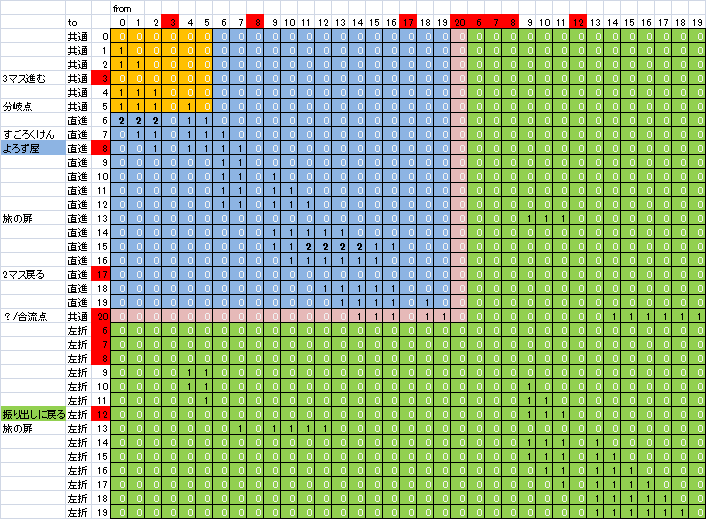
最後に、δを計算するために用いた行列を画像ファイルとして添付しておきます。
付録5 すべてを厳密に計算するには (2011.10.28追記)
付録2、付録3に示したように、複数回ループも、サイコロ回数変動も、厳密に取り扱うことが可能です。したがって、すごろくのマス目とサイコロの回数が有限である限り、行列を拡張することで厳密に計算することが可能です。
ここでは、実際に計算は行いませんが、そのアイデアだけ紹介します。アイデアといっても、付録2、付録3で示したものとほぼ同様ですので、詳しくはそちらの記述も参照ください。
もうこの際、ゴールまで含め、そして分岐まで含めて、すべてのマス41に対して確率分布を考えてしまいましょう。こうすると、「よろず屋」だけでなく、「ゴール」に到達する確率など、好きな確率が求められます。
そして、サイコロの回数は、7~15回くらいになるはずですので、9つのすごろく場の分考えます。
41×9=369 つまり、369次元ベクトルで確率分布を表し、369×369行列で、時間発展を表します。この行列を15乗して適切なところまで和を取ればよいだけです。
なお、この節で議論した、7~15や、41×9などの値はざっと計算しているので実際とは異なるかもしれませんが、それが議論の本質に影響しないことは(ここまで議論についてきてくださった読者の方には)伝わると思い、考察を終えたいと思います。
また、本ページは、ここで示した方法で「計算できる」ということを紹介しているだけです。これよりもエレガントな方法があるような気がします。ご存じの方は、掲示板等で教えていただけると嬉しいです。
おわりに
感想など
前半の確率計算は高校数学のような内容です。もっと良い計算方法があるかもしれません。複数回試行する際には、「少なくとも1回成功する」という事象よりも、「1回も成功しない」という事象のほうが純粋種のイメージなので確率も求めやすい、という方針のもと計算方法を考えています。
行列計算は、ゲーム関連の活動には初めて使いました。エクセルが非常に便利です。
このページで紹介した手法は、この程度の単純なモデルであれば応用が効くかと思います。需要が少なそうですが(笑)
やり込み、その他への効率化のヒントになれば幸いです。 なお、計算ミス等あれば指摘いただけると助かります。
2011.10.28 - 2011.10.23 右弐
参考情報
■プレイヤー
○ 腹黒パンダ 様 該当のblog記事
「ふりだしに戻る」を期待したリカバリー策について参考にさせていただきました。
■書籍
○ ドラゴンクエストVのあるきかた(CB's PROJECT 著)
オラクルベリーのすごろく場の「?」のマスで出る効果について参考にさせていただきました。
また、すごろく場における敵との遭遇率を参考にさせていただきました。
○ ドラゴンクエストV 天空の花嫁公式ガイドブック上下巻プレイステーション2 版(スクウェア・エニックス)
(すごろくけん)を落とす敵の情報を参考にさせていただきました。
関連情報
○ 物理数学の直観的方法 第2版(長沼 伸一郎 著)
理工系の大学生には有名と思われる本です。第11章にて「作用マトリックス」という名前で上述の議論と似た行列の使い方の話が紹介され、初学者にもわかりやすい記述となっています。
|
▲ 日記へ戻る ▲ メインページへ戻る 感想・質問・注文・呪文はこちら⇒掲示板 | スポンサーサイト広告(提供:Amazon) |
